Numbers & Counting | Arithmetic | Fractions & Decimals | Prealgebra | Site Map

Switching Directions

Let's finish up by looking at the number line again. You have been bouncing left and right. On the number line, every time you switch symbols, you change direction.

When you add (+ symbol), you move to the right.


When you subtract (- symbol), you switch directions and move to the left.


As we showed you before, when you add a negative number, you also move to left. All the negative numbers are to the left of the zero point. Using the idea above, when you subtract a negative number, you change direction twice. That first minus sign makes you go to the left and the second one switches direction so you go to the right.


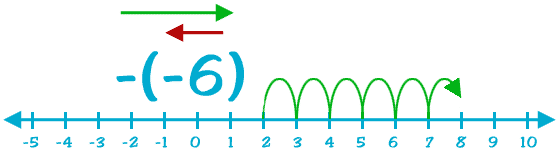
We're just offering you another way to think about multiple signs in addition or subtraction problems. "+" goes right and "–" switches direction. Two "–" symbols makes you switch twice.

More than One Value

So let's look at a couple of examples with three values before we finish. You already know how to subtract with three values. Start with the first two values on the left and then do one more at a time.

18 - 6 - 5 - 4 = ?
Let's convert it into a format with negative numbers. You have done this.
18 + (-6) + (-5) + (-4) = ?
If you add up those negative values you get (-15).
18 - 15 = 3.

What about with negative numbers?
2 - 6 - (-4) - (-3) = ?
Let's fix all of those double negative signs.
2 - 6 + 4 + 3 = ?
And now what does this look like on a number line?


Can you start to see how this all works? Positive values go left and negatives switch directions. Can you figure out this problem?

2 + (- (- (- (-2)))) = 4 (see how there are four minus signs?)

It's honestly a horrible problem. No mathematician would ever write that. Let's call it a brain teaser instead.

Related Links