Numbers & Counting | Arithmetic | Fractions & Decimals | Prealgebra | Site Map

Time for the Number Line

In the world of numbers, you will usually work with whole numbers. Those are the numbers that are zero and greater on a number line. There are no parts of numbers to worry about with whole or natural numbers. When you start to work with integers, you will start using numbers that are less than zero. For example, you might have -3, -25, or -147. Once you start working with integers, you'll also be adding negative and positive numbers. The easiest way to look at addition with negative numbers is to use a number line.


You've seen these lines before, but now that we have negative numbers, we can count values below zero. They are still numbers that are "whole" (not parts of numbers), but they have negative symbols in front of them. When you count, add, or subtract, you will bounce around the line as you always have. Positive numbers bounce to the right and negative numbers will bounce to the left.

Bouncing Left and Right

We'll begin with an easy idea. Let's say you start with positive 6 and you want to add a 4. Your point starts on the value for six and then bounces to the right four spaces. You've done that a bunch of times by now. You just added four to six.


When you add a negative number, you want to bounce to the left. Let's say you start with positive 6 and you want to add a negative 4. Your point starts on the value for six and then bounces four spaces to the left. You just added six and negative four.


Your sums will not always stay greater than zero. Let's start with 4 and add a negative 6. You start on the four and bounce to the left six spaces. It will take you past the zero and down to negative two. This will happen when you work with integers. You will move from positive to negative values or negative to positive values all of the time.


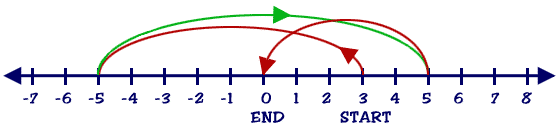
More than One Value In your earlier work with multiple addends you used positive numbers, but you can have multiple addends that are both positive and negative. You might be asked to add positive 3, negative 8, positive 10, and negative 5. The problem would look like this...

3 + (-8) + 10 + (-5) = ?

Whip out that number line and start the bouncing ball. Start on the 3, go left 8 jumps, go right 10 jumps, and finish by going left 5 jumps. You should wind up at 0.

Now Without the Line

We want you to try some of this without a number line. We'll keep the examples easy.

Example:
5 + (-8) = ?
Think of it this way... 5 + (-5) + (-3)
Those values of five cancel each other out and you are left with a -3.
5 + (-8) = -3

You're probably starting to see how adding positive and negative numbers is like subtraction. It is. The reason we are looking at negative numbers this way is to show you that they are independent values. A math problem like 3-7 is nothing more than the addition problem 3+(-7). If you start thinking about negative numbers as separate values now, it will make math easier later. For example, when you start with multiplication, negative values must stand on their own.

Example:
5 x -4 x 6 x -2
If you were sloppy and wrote it out this way, you might have trouble solving the problem. Are those subtraction operations or negative numbers? This would make life so much easier...
5 x (-4) x 6 x (-2)

Overall, we want you to think about how you add negative numbers and positive ones. The whole idea of negative numbers is a big conceptual jump in math and you are awesome for thinking about it now.

Example:
-4 - 5 = ?
Think of it as two negative numbers.
(-4) + (-5) = (-9)

Related Links