Types of Numbers
We've been talking about numbers in all of other pages. Your head is filled with numbers right now. As the field of math was growing, mathematicians needed to classify those numbers so they'd be easier to work with. They started by classifying the easiest numbers first. It's similar to the way that you start with the easiest numbers in your problems. This page will give you a quick overview of numbers. We have more detail about many of these number types in the next few pages.Natural Numbers
Natural numbers are the numbers you use every day. These numbers include values from one all the way up to infinity. The numbers you can count with your fingers and toes are all natural numbers.Natural Number Examples: 1, 2, 5, 18, 150, 1,586, 258,569.

Whole Numbers
Whole numbers are just like natural numbers except that they also include 0. Did you know that ancient mathematicians worked for a long time before they used the concept of 0? Eventually, they realized they needed a value that represented no amount.Whole Number Examples: 0, 1, 2, 5, 18, 150, 1,586, 258,569.

Integers
Did you notice how those number lines all started at 0? Number lines with integers can have every positive and negative number. When we put in the negative numbers, we made the set of integers. Integers include all of the numbers from negative infinity to positive infinity.Integer Examples: -258,589, -1,586, -150, -18, -5, -2, -1, 0, 1, 2, 5, 18, 150, 1,586, 258,569.
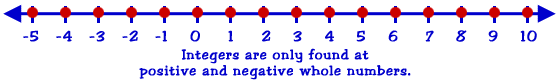
We've been throwing around the word "infinity", but we never really explained the term. Infinity represents a value that is too high or too low to count. It's a number that goes on forever. If you have a number with five million digits, infinity has more. It's an infinite value. When you see infinity written out, it will look like the number 8 on its side, like this: ∞.
Evens and Odds
We may have talked about them before, but we're going to remind you about even and odd numbers. Even numbers can be divided by two and have no remainder. Odd numbers have a remainder of 1 when you divide by 2. It doesn't matter if they are positive or negative.Even Number Examples: -18, -6, 2, 8, 256
Odd Number Examples: -55, -47, -5, 3, 453, 1,536,859
Rational Numbers
We cover fractions in another section. You've probably heard of them before. Another term for a fraction is a rational number. The word rational comes from the word ratio. In the case of rational numbers, it is a ratio of two integers. The integer on top is called the "numerator" and the integer on the bottom is called the "denominator". There is an extra rule you must remember. The bottom number can never be 0. If there is a 0 on the bottom, the division doesn't work. We'll get into the math of fractions and decimals in other sections. Just know that a rational number is one integer on top of another in a fraction.Rational Number Examples: 16/5 = 3.2, 1/5 = 0.2
16 and 5 are both integers.

Prime and Composite Numbers
You may have heard of prime numbers. Prime numbers are special because they can only be divided evenly by 1 and themselves. A number like six can be divided by 1, 6, 2, and 3. There will be no remainder when you divide by those numbers. A prime number like 7 can only be divided by 1 and 7 without a remainder. We'll talk more about prime numbers in a bit. Here's a list of easy ones.Prime Number Examples: 2, 3, 5, 7, 11, 13, 17, 19.
The opposite of a prime number is a composite number. We talked about how six can be divided by 1, 6, 2, and 3. Six is a composite number because it is divisible by many different numbers and has no remainder. All even numbers after 2 are composite numbers because they all have 2 as a factor (look in the factoring section for more info).
Composite Number Examples: 4 (2*2), 6 (2*3), 8 (4*2), 15 (3*5), 33 (11*3)
NOTE: Remember that the asterisk or star symbol stands for multiplication.
Compatible Numbers
There isn't a real math category for compatible numbers, but you might hear about them. These numbers are compatible with you. These are numbers you can easily multiply and divide. For most of us, that includes numbers like five, ten, and twenty-five. We use those numbers all the time for values of money (nickels, dimes, and quarters). We think really quickly with those numbers. If you had us try to do multiplication with 17 and 23, it would take us a lot longer. Compatible numbers are different for every person. You might like multiplying by 17.Opposites
Let's finish up with one last term. Opposites are a pretty easy topic. You know about negative and positive numbers. The opposite of a positive number is the negative. The opposite of the negative is the positive. Once you change the sign of your original number, you made the opposite value.Opposite Number Examples: -2 and 2, -589 and 589, -4,587 and 4,587.
► NEXT PAGE ON FRACTIONS & DECIMALS
► NEXT STOP ON SITE TOUR
► RETURN TO TOP OF PAGE
► Or search the sites...
► NEXT STOP ON SITE TOUR
► RETURN TO TOP OF PAGE
► Or search the sites...

- Overview
- Number Types
- Factors
- Fractions
- Decimals
- Percentages
- Estimation
- Ratios
- Money
- Activities
- More Maths Topics

Useful Reference Materials
Wikipedia:https://en.wikipedia.org/wiki/Fraction_%28mathematics%29
Encyclopædia Britannica:
http://www.britannica.com/topic/fraction
University of Delaware:
https://sites.google.com/a/udel.edu/fractions/